Una Pelota de Béisbol Hecha de Neutrones
¿Te imaginas a una pelota de béisbol hecha de neutrones totalmente? Pues en teoría debes saber que sería una masa impresionantemente grande. Lo describiremos a continuación.
Los neutrones son partículas atómicas que al igual que los protones, se encuentran en el núcleo de los átomos. Por esta misma razón se les conoce como nucleones en su conjunto.
¿Cuál es la masa de un neutrón?
Según reporta el libro Física Universitaria con Física Moderna de Sears-Zemansky 12va Edición Volumen 2, en su versión en español, en su página 1469 los valores de las masas de las partículas atómicas son los siguientes:

Como puedes ver, los valores de las masas son relativamente pequeños comparado con los objetos cotidianos a los que estamos acostumbrados a manipular. Lo que estamos analizando es una pelota de béisbol hecha de neutrones completamente. Así que lo que sigue es investigar el volumen de una pelota de béisbol.
¿Cuál es el volumen de una pelota de béisbol?
Según la regla 1.09 de la MLB dada en el año 2016 la pelota debe tener un perímetro no menor de 9 pulgadas y no mayor a 9 1/4 de pulgadas. Manejaremos el valor mínimo de 9 pulgadas de perímetro. De esta manera tendríamos un diámetro dado por la ecuación siguiente,
![]()
![]()
Con este dato del diámetro podemos calcular el valor aproximado del volumen de la bola con la siguiente fórmula,
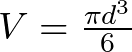
Sustituyendo el valor aproximado del diámetro en pulgadas de la pelota de béisbol,
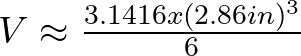
![]()
Hasta aquí con el asunto del volumen de una pelota de béisbol. Ahora en la siguiente sección analizaremos el tamaño de cada neutrón si se coloca uno tras otro para llenar el volumen de la pelota.
Tamaño de un neutrón
No es un tema popular que te lo puedas encontrar en los buscadores de Internet hoy en día. Al menos no de forma directa. Pero investigando bien puedes encontrar que el tamaño aproximado de un neutrón es cerca de un fermi, es decir,
![]()
En el blog de Rama Nujan está un post que habla de las relaciones de tamaño de las partículas subatómicas. En este post menciona que el tamaño del protón y neutrón son aproximadamente los mismos.
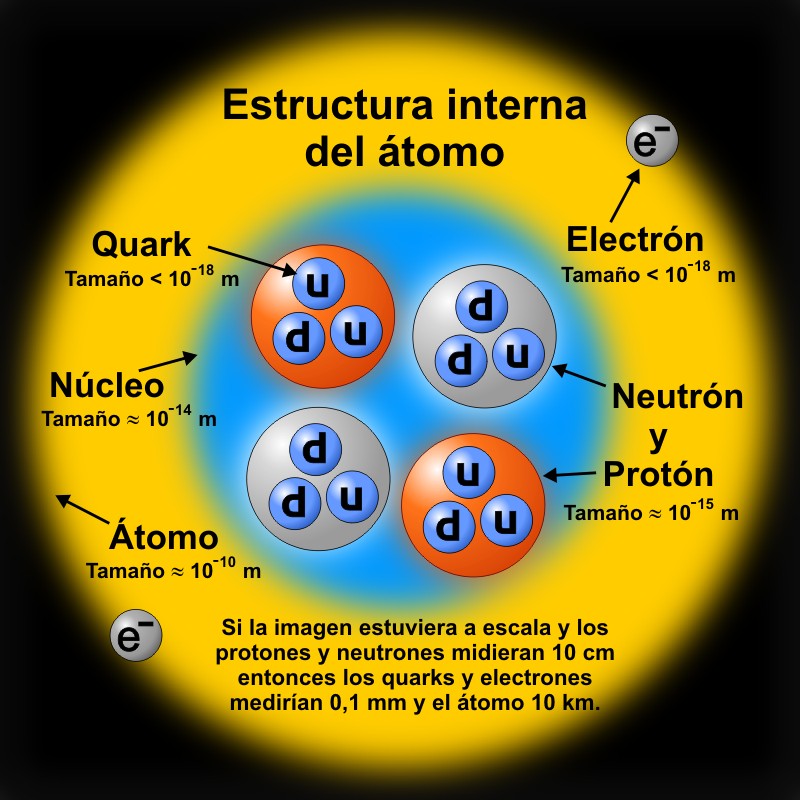
Manipulando los volúmenes
Convirtiendo el volumen de la Pelota de Béisbol a metros cúbicos
Puesto que manejaremos el diámetro del neutrón en metros y por ende al calcular el volumen de este en metros cúbico entonces requerimos tener el volumen de la pelota de béisbol en las mismas unidades.
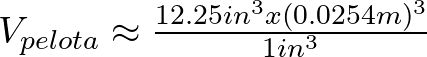
![]()
Calculando el volumen de un neutrón
Para el neutrón ya vimos que su diámetro aproximado es un fermi. Entonces con este dato calculamos el volumen aproximado de la siguiente manera,
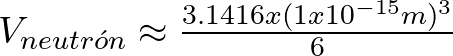
![]()

Construyendo la pelota de neutrones
Si llenamos el volumen de la pelota con neutrones tendríamos el siguiente número de neutrones aproximadamente omitiendo los espacios intersticiales entre neutrones.
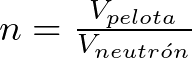
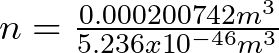
![]()
¿Qué masa tendrá esta pelota de neutrones?
Al estar compuesta de neutrones esta pelota tendrá una masa dada por los siguientes cálculos,
![]()
![]()
![]()
Tal masa es unos 1,070,245 millones la masa de las Torres Petronas.

Esta pelota de neutrones tendría una masa muy grande
La masa de la pelota hecha de neutrones deberá tener una masa de,
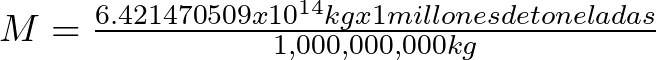
![]()
![]()

Efectos gravitatorios sobre una persona de 70 kg
Con esta gran masa una persona que se encuentre inicialmente a 100 metros de distancia de esta pelota sentiría una fuerza dada por la Ley de la Gravitación Universal como,
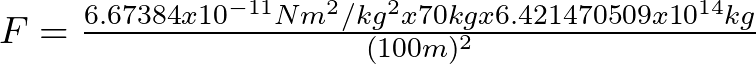
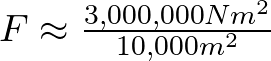
![]()
Esta fuerza en kilogramos es,
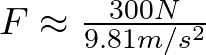
![]()

Efectos gravitatorios sobre una persona de 70 kg a 10 metros y a 1 metro.
Cada vez que la persona se vaya acercando a la pelota de neutrones:
a 10 metros,
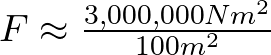
![]()
con una fuerza en kilogramos de,
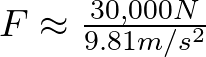
![]()
a 1 metro,
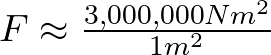
![]()
con una fuerza en kilogramos de,
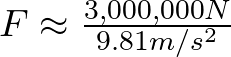
![]()
es decir,
![]()
Con esta fuerza la persona de 70 kg sería aplastada totalmente. Solo a 100 metros sentiría una fuerza de 30 kg aproximadamente a la cual podría escapar si así quisiera. Pero a 10 metros ya estaría bajo una fuerza arriba de 3 toneladas lo cual le sería imposible escapar al campo gravitatorio de una pelota de béisbol hecha de neutrones.