¡Compártelo!

Número de Visitas: 1.070

4.7/5 - (10 votos)

Diseño de un sistema hidráulico

El diseño de un sistema hidráulico requiere de conocimientos básicos del Principio de Pascal. Este principio nos describe cómo es que con una fuerza relativamente pequeña se puede generar una fuerza mucho más grande. Esto se aplica en el levantamiento de objetos muy pesados. Un ejemplo claro es la aplicación en los sistemas hidráulicos que se usan en los talleres de afinación automotriz. Habrán visto cómo tienen a los automóviles levantados con un pistón para poder explorarlos por la parte de abajo con mayor facilidad.

Problema

Supongamos que queremos hacer el diseño de un sistema hidráulico el cual debe levantar un peso máximo de 7 toneladas. Para esto debemos tomar en cuenta que el pistón máximo que se puede conseguir en el mercado tiene un diámetro de 50 cm. Además el pistón pequeño de bombeo puede ser de 10 cm de diámetro.

¿Cuánto debe ser el valor de la fuerza en el pistón pequeño para levantar la 7 toneladas?
Si las 7 toneladas se levantan 5 m, ¿cuánto volumen de líquido hidráulico aumenta en el contenedor del pistón grande si el diámetro del contenedor es de 0.5 m?

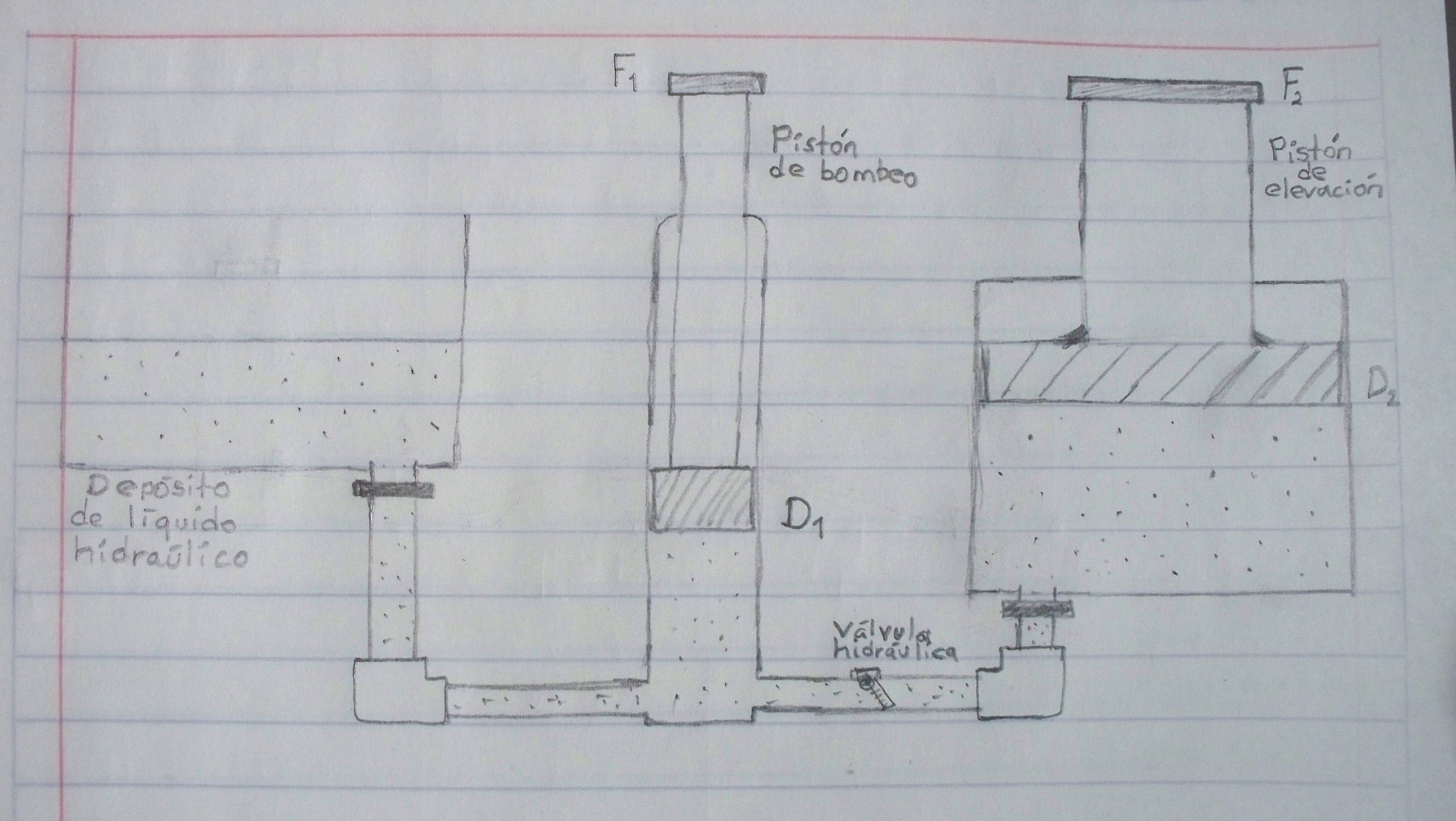
Solución

Para la primera pregunta debemos considerar el Principio de Pascal como sigue,

$\frac{F_{1}}{D_{1}^{2}} = \frac{F_{2}}{D_{2}^{2}}$

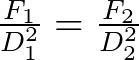
despejamos a la fuerza correspondiente en el pistón pequeño,

$F_{1} = \left(\frac{D_{1}}{D_{2}}\right)^{2}F_{2}$

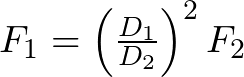
Los datos que tenemos son,

$F_{2} = 7 \hspace{1mm}ton$

$D_{1} = 10 \hspace{1mm}cm$

$D_{2} = 50 \hspace{1mm}cm$

Sustituyendo en la fórmula anterior,

$F_{1} = \left(\frac{10 \hspace{1mm}cm}{50 \hspace{1mm}cm}\right)^{2}7 \hspace{1mm}ton$

$F_{1} = 0.28 \hspace{1mm}ton$

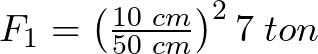
Considerando que,

1 ton = 1,000 kg

entonces multiplicamos por 1,000 a 0.28,

$F_{1} = 280 \hspace{1mm}kg$

Esta es la fuerza que se requiere aplicar sobre el pistón pequeño para bombear y al mismo tiempo levantar el pistón grande con 7 toneladas. Suena una ganga de fuerza. Pero el precio que hay que pagar es que el pistón pequeño requiere desplazar mucho más líquido hidráulico que el pistón grande. En la siguiente pregunta veremos algo relacionado con esto.

Para la segunda pregunta consideraremos el volumen del contenedor del pistón grande. El volumen de un cilindro está dado por,

$V = \frac{ \pi D^{2} h}{4}$

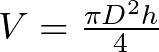
Los datos son,

$h = 5 \hspace{1mm}m$

$D = 0.5 \hspace{1mm}m$

Sustituyendo los datos,

$V = \frac{ 3.1416 (0.5 \hspace{1mm}m)^{2} (5 \hspace{1mm}m)}{4}$

$V \approx 0.98175 \hspace{1mm}m^{3}$

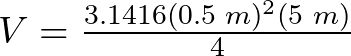
considerando que el contenedor del pistón pequeño tiene un diámetro de 0.10 m y una altura de 3 m, el volumen de este contenedor es,

$V = \frac{ 3.1416 (0.10 \hspace{1mm}m)^{2} (3 \hspace{1mm}m)}{4}$

$V = 0.023562 \hspace{1mm}m^{3}$

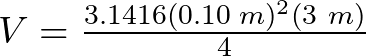
Y así podemos saber cuántas veces aproximadamente se tuvo que bombear desde el contenedor pequeño hacia el contenedor grande para poder levantar los 5 m al objeto de 7 toneladas. Calculamos tales veces con,

$n = \frac{Volumen incrementado del contenedor grande}{Volumen del contenedor pequeño}$

$n = \frac{0.98175 \hspace{1mm}m^{3}}{0.023562 \hspace{1mm}m^{3}}$

$n \approx 42$

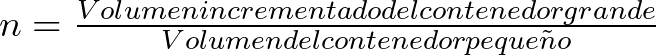
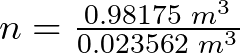
A este precio nos referíamos anteriormente. Si, levantamos 7 toneladas con solo 280 kg de fuerza pero hay que aplicarla bombeando el líquido hidráulico aproximadamente 42 veces. Bombeando 42 veces desde el contenedor pequeño hacia el contenedor grande para levantar a este objeto pesado una altura de 5 m.

Diseño de un sistema hidráulico

Problema

Solución

Javier Rivera

Puede que también te guste

Presión Hidrostática Sobre Un Submarino