Caída Libre de una Pelota de Béisbol
El béisbol es uno de los deportes mejor pagados en los Estados Unidos de América en la MLB(Major League Baseball). Muchos jugadores de diferentes países, especialmente latinos, logran el éxito deportivo al ser convocados por uno de los equipos de esta liga. La MLB cuenta actualmente con 30 equipos divididos entre la Liga Nacional y por otro lado la Liga Americana. En este deporte es muy común que se presente el problema de la caída libre de una pelota de béisbol. Por ende, es preciso analizar este problema de física en esta ocasión.

Caída Libre de la Pelota
Supongamos que se deja caer desde el reposo a una la pelota de béisbol desde una altura de 20 metros y deseamos saber las siguientes características:
a) ¿Cuánto tiempo tarda en golpear el suelo?
b) ¿Con qué velocidad golpea al suelo?
c) ¿Qué velocidad lleva a la mitad de su caída?
Así que tenemos que usar 3 fórmulas para dar respuesta a este problema.
Solución
Lo primero es que debemos encontrar cada fórmula de las preguntas anteriores.
a) Usaremos la fórmula:
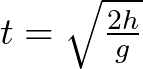
Los datos son:
![]()
![]()
Sustituyendo los datos en la fórmula,
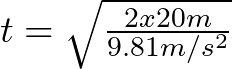
t = 2.02 s
Nota que en la caída libre de una pelota de béisbol o de cualquier objeto se toma con valor positivo a la aceleración de la gravedad porque así va aumentando la velocidad cada segundo que cae la pelota. Cuando la pelota va hacia arriba se le llama tiro vertical y ahí la aceleración de la gravedad se toma como negativa ya que va disminuyendo a la velocidad cada vez que avanza a más altura hasta llegar a detenerse totalmente para después regresar en caída libre.
b) La fórmula es,
![]()
Sustituyendo los datos,
![]()
v = 19.81 m/s
Con los casi 20 m/s la pelota golpea el suelo al caer desde una altura de 20 m.
c) Tenemos la fórmula siguiente,
![]()
dado que el tiempo es la mitad del tiempo calculado en el inciso a) y también que a la mitad de la caída libre ha caído 10 m, aunque éste último dato no es requerido. Entonces se usa,
![]()
![]()
![]()
de esta manera ya podemos sustituir en la fórmula de la velocidad final,
![]()
![]()
Por lo tanto, ya hemos respondido a las tres cuestiones de los incisos del inicio del problema.
Si tienes alguna duda puedes expresarla en los comentarios.