El Saque de Meta como Proyectil
El tiro parabólico o el movimiento de un proyectil en un plano es uno de los temas en los el efecto de la gravedad es el factor protagonista. El saque de meta que ejecuta un portero en el fútbol soccer es un ejemplo muy claro de este tipo de movimiento.
Saque de Meta
El portero de cierto equipo popular de la Liga MX en México ejecuta el saque de meta pateando al balón con una fuerza tal que éste sale disparado a una velocidad inicial de 14.45 m/s. La pelota sale con un ángulo de inclinación con respecto a la horizontal de 35°. Calcular la distancia a la cuál caerá el balón, la altura máxima que alcanza y el tiempo de vuelo de la pelota.
Solución
Lo primero es que hay que tener muy clara la fórmula que podemos usar para darle solución a este problema. A continuación la 3 fórmulas necesarias:
![]()
![]()
![]()
De esta forma podemos aplicar tales fórmulas de la siguiente manera. Primero calcularemos la distancia a la cual cae el balón con la primer fórmula como sigue.
Sabemos que los datos son:
![]()
![]()
![]()
Sustituyendo estos datos en la primera fórmula,
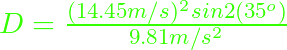
D = 20 m
Ahora calcularemos la altura máxima a la que se levanta el balón. Sustituimos valores en la ecuación de H,
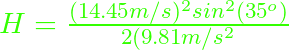
H = 2.66 m
Y finalmente calcularemos el tiempo de vuelo del balón. Sustituimos los datos en la última ecuación del tiempo T,
![]()
T = 1.69 s
De esta manera pudiste ver el cómo se resuelve el problema del saque de meta en el que se ejemplifica muy bien el movimiento de un proyectil.
Otros problemas:
1. Convertir Millas a Kilómetros